Think about the problem 13 x 14 for a moment.  Does your brain tell you to reach for a piece of paper?  A calculator?  Do you start solving for partial products in your head [(13x10) + (13x4)]?  Or do you visualize an array for 13 x14?  What would be the most efficient way to solve this problem?  If you have read my blog post, “What is an array in math?”  you are ready to start thinking about a math array example with bigger numbers.  

Many of us learned to solve two-digit by two-digit multiplication problems by using the standard algorithm.  While the standard algorithm works, it is just a memorized procedure that doesn't maintain the place value of the numbers. Because of this, the standard algorithm is often confusing to students and fraught with errors. Once students have used multiplication arrays to build a foundation of understanding, however, then they can use the standard algorithm more successfully.

Building an Array for a Two Digit Times Two Digit Problem

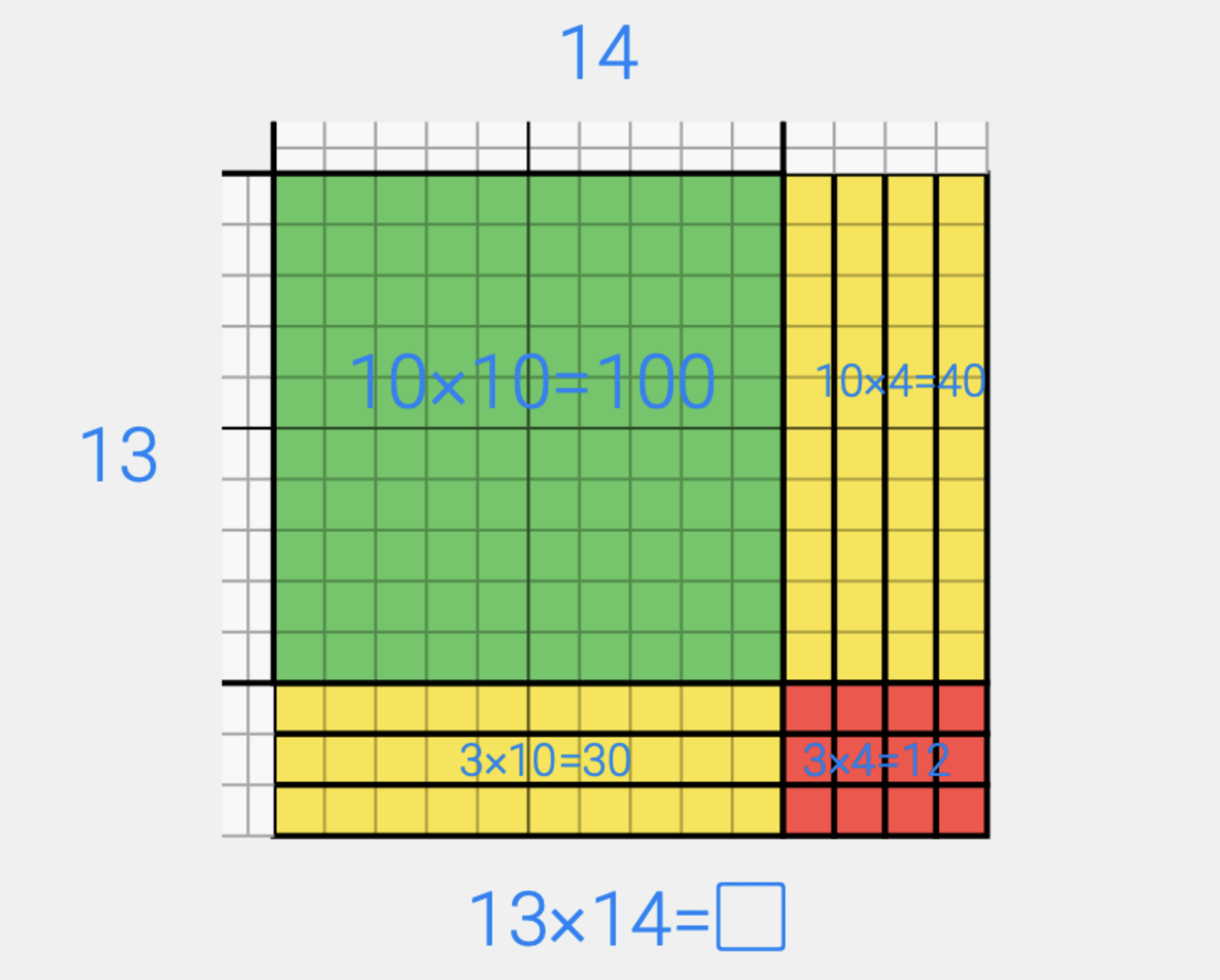
Just like we did with the small arrays, we will use the idea of building a model that has the dimensions of the problem.  This model will be 13 tall and 14 wide. The value of all the squares in the middle is our product.

Using Partial Products

Then, we can break the array into pieces to find the product.  We can us the four partial products to find our solution. (These are the same partial products that you are finding when you use the standard algorithm.)

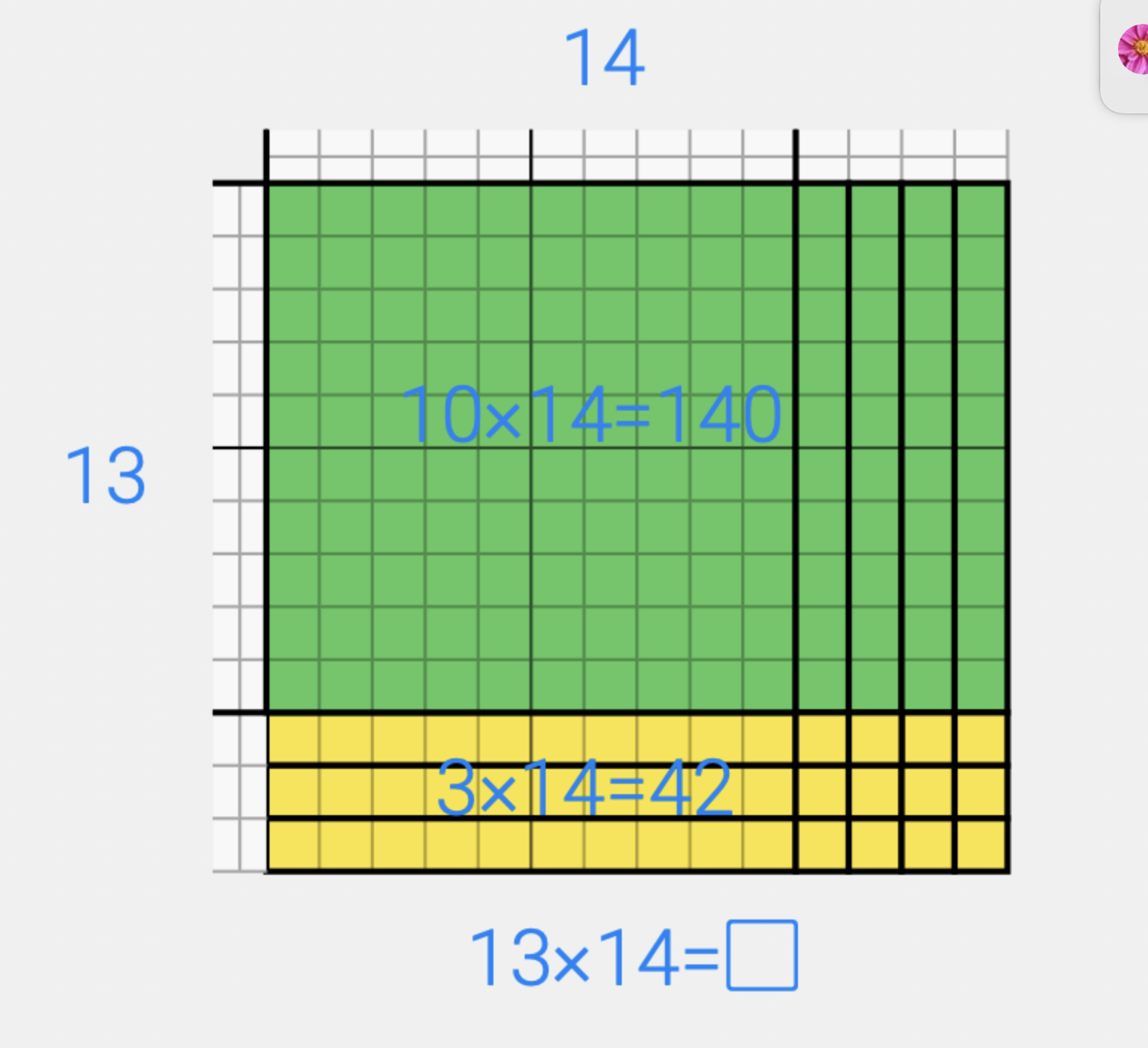
We could also break the problem into two pieces.  I have found this is the method I most often use now when I am solving problems mentally.  So I would think of this problem as [(13x10) + (13x4)]. I never knew that you could break a multiplication problem into two parts but our array proves that will still get the same answer and the problem is much easier to solve. 

Having multiple options allows us to think flexibly about how to solve a problem and use the best strategy for the numbers involved.

Build Your Own Math Array Example

Build your own math array. The Number Pieces App from the Math Learning Center makes it easy, even if you don't have base ten pieces at home. Can you build an array for 14 x 15? Use colors to show how you would break it down. Will you think about it as four partial products or two? How will the model change if you want to build a problem with larger numbers, like 21 x 23? How is your understanding of multiplication changing as you make a math array examples?

If you would like to learn more about how children’s understanding of multiplication develops, I highly recommend this video by Graham Fletcher.